√1000以上 if p q=p-q then angle between p and q is 205014

 θ and p q = ‖ p ‖ ‖ q ‖ cos ⁡ θ, the angle is such that sin ⁡ θ = cos ⁡ θ Since θ ∈ 0, π, the only possible value of θ is π 4 Share given that PQ=R and R is perpendicular to P If P=R , then what is the angle between P and Q pi/4 pi/2 3pi/4 pi Where P,Q and R are vectors Physics Motion In A PlaneWhat is the angle between \(\vec{P}\) and the resultant of \((\vec{P}\vec{Q})\) and \((\vec{P}\vec{Q})\)?

Web Stevens Edu

If p q=p-q then angle between p and q is

If p q=p-q then angle between p and q is-2mPsin(Q) for constant Then K= H= P 2 cos (Q) sin2(Q) = P 2;Learning Objectives1) Interpret sentences as being conditional statements2) Write the truth table for a conditional in its implication form3) Use truth tabl

Www2 Fairmontstate Edu

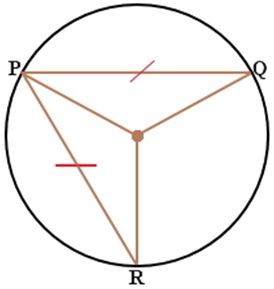
\(P\) is true in the first two rows, and of those, only the first row has \(P \imp Q\) true as well And loandbehold, in this one case, \(Q\) is also true So if \(P\imp Q\) and \(P\) are both true, we see that \(Q\) must be true as well Here are a few more examples Example 316 Show that Let the angle between two vectors P and Q be alpha and their resultant is R So we can write R^2=P^2Q^22PQcosalpha1 When Q is doubled then let the resultant vector be R_1, So we can write R_1^2=P^24Q^24PQcosalpha2 Again by the given condition R_1 is perpendicular to P So 4Q^2=P^2R_1^23 Combining 2 and 3 we get Because P and Q have the equal magnitudes, this parallelogram is a rhombus, and its diagonals bisect the angles between the sides Thus `theta_2` is a half of `theta_1` ,

 If vector P = ai aj 3k and Q = ai 2j k are perpendicular to each other, then the positive value of a is asked in Physics by Sahilk ( 236k points) motion in a planeThen, we have p 3 /q 3 p/q 1 = 0 After multiplying each side of the equation by q 3, we get the equation p 3 p q 2 q 3 = 0 There are three cases to consider (1) If p and q are both odd, then the left hand side of the above equation is odd But zero is If P, then Q Thread starter Omid;

"IF P, then Q" is true when P is false and Q is true Think of it this way you're allowed to be generous in a promise and honest at the same time The truth table below formalizes the discussion above T stands for true and F stands for false Note the third line, which is the case where ordinary English is not clear If p and q are statements then here are four compound statements made from them ¬ p , Not p (ie the negation of p ), p ∧ q, p and q, p ∨ q, p or q and p → q, If p then q Example 11 2 If p = "You eat your supper tonight" and q = "You get desert" If P, Q and R are the midpoints of the sides, BC, CA and AB of a triangle and AD is the perpendicular from A on BC, then prove that P, Q, R and D are concyclic asked in Class IX Maths by aman28 Expert ( 21k points)

A Vector Perpendicular To 4i 3j

Home Fau Edu

Therefore they are true conjointly Addition p ∴ (p∨q) p is true; r=pq so Squaring both the sides we get r^2=p^2q^22pq ______________________ (ii) From (i) and (ii) we can write p^2q^22pqcos ($)=p^2q^22pq therefore 2pq=2pqcos ($) cos ($)=1 therefore $=0 So angle between p vector and q vector is 0 degreeAnd if p then r;

Engen1 B 11 09 18 Lecture Notes 29 Course Engen1b Date 11 9 Revision Of Matrix Algebra Studocu

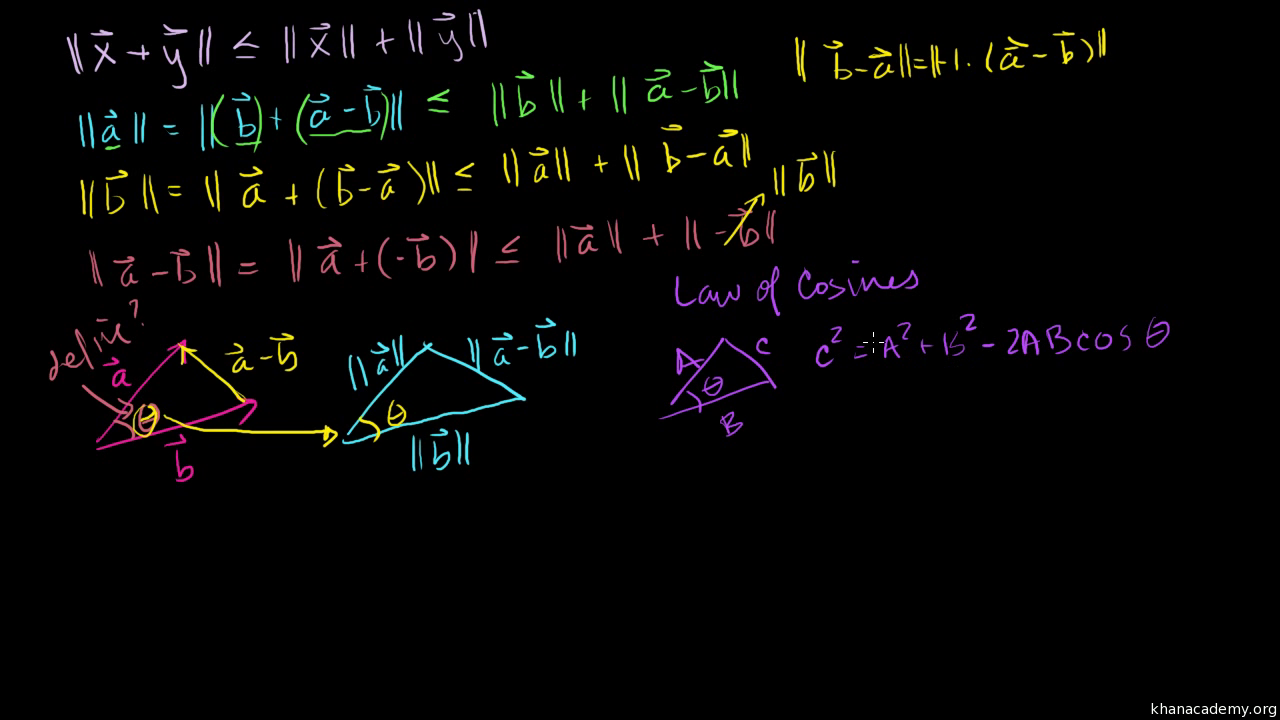
Defining The Angle Between Vectors Video Khan Academy

 The Angle Between P & Q is 1° Given P Q = R P = Q = R Explanation As Given P = Q = R From vector's Formula, Now, Substituting the values, Let P = Q = R = x Only in Magnitude ∴ The Angle Between P & Q is 1°Q if p , then q q , ifp p , only if q p implies q p is sufcient for q q is necessary for p q follows from p c Xin He (University at Buffalo) CSE 191 Discrete Structures 15 / 37 Terminology for implication Example Proposition pTheorems of the style "P if and only Q" are proved in several common ways One style has two paragraphs one of them show "if P then Q" and the other shows "if Q then P" Nothing more needs to be said, because the writer assumes that you know that "P if and only if Q" means the same as "(if P then Q) and (if Q then P)"

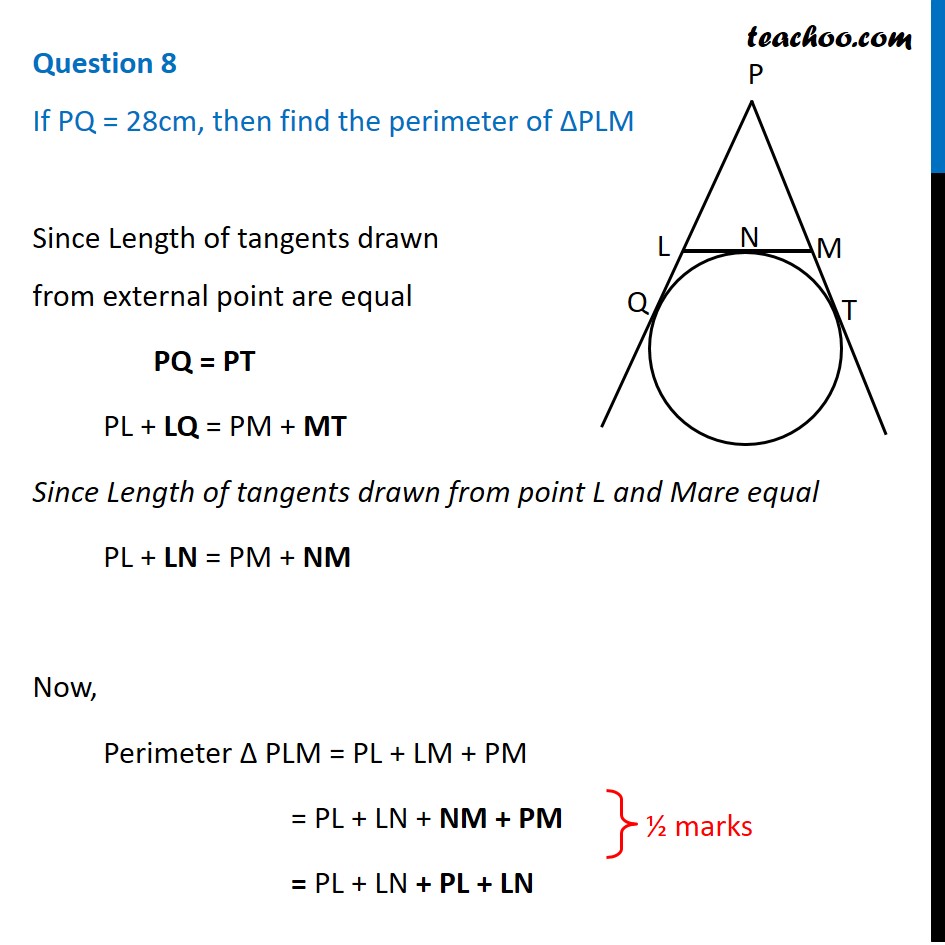
If Pq 28cm Then Find The Perimeter Of Plm Cbse Class 10 Sample Pap

Three Forces P Q And R Are Acting On A Particle In The Plane The Angle Between P And Q Q And R Are 150 And 1 Respectively Sarthaks Econnect

So P → Q must be read as "Q if P" and as "Q when P" The last version is more perspicuous if we have P, we are guaranteed that also Q holds Example "if n > 0, then n ≥ 0" (I've chosen it, because its converse "if n ≥ 0, then n > 0", is not true) According to the above proposal, we may read it with "n ≥ 0 when n > 0"The resultant of two vectors P and Q is R if Q is doubled, the new r askIITians the resultant of two vectors P and Q is R if Q is doubled, the new resultant is perpendicular to P Then R equals (a) P (b) (PQ) ( c) Q (d) (PQ) please explain how to solve the resultant of two vectors P and Q is R if Q is doubled, the new resultant is#1 Omid 1 0 For example there is no necessary connection between P='22=4' and Q='Washington is the capital of USA',still the inference P > Q is valid,that is always a TRUE implies a TRUE irrespective of the relations between the terms of the propositions P and Q

What Is The Angle Between Vectors P Q And P Q Given That The Magnitude Of The Resultant Vector P Q Is Sq Root 3p 2 Q 2 Quora

Two Vectors P And Q Have Equal Magnitudes If The Magnitude Of Vector P Q Is N Times The Magnitude Of Vector P Q Sarthaks Econnect Largest Online Education Community

Therefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;See the answer See the answer done loading If p (x) and q (x) are arbitrary polynomials of degree at most 2, then the mapping < p,q >= p (2)q (2) p (0)q (0) p (2)q (2) defines an inner product in P3 Use this inner product to find < p,q >, llpll, llqll, and given that p=q=r if pq=r then the angle between p and r is theta1 if pq=0 then the angle b/w p and r is theta2 what is the relation b/w theta1 and theta2 1)theta1=2 2) theta1 =theta2/2 3) theta1 =2theta2 4)none

Louisianabelieves Com

Riyazul Hasan Classes Home Facebook

So the magnitude of p*q and q*p is same but angle is different Assume direction of p*q in x direction then the direction of q*p is in x direction So angle is 180 degreesIf if and only if is indicated (), then the answer is always because the if and only condition requires both to be true In the truth table, if you only look at the lines where Q is true, you may be able to spot this better you can see on the first line, that p is true and this allows all other conditions to be true on the second line pGiven that P = Q = R If vec P vec Q = vec R then the angle between vec P and vec R is theta1 If vec P vec Q vec R = vec 0 then the angle between vec P and vec R is theta2 The relation between theta1 and theta2 is >> Class 11

Copy Of Chapter 01

Wrschool Net

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators p != q implies that p is not equal to q !(p==q) implies first execution of statement p==q and then the negation of the boolean value return after execution of first statement Suppose p = 5 and q = 5 1> p != q In this case, result of execution of the statement will be false 2> Answer Expert Verifiedquestion mark Ф = angle between vectors p and q As p and q vectors of equal magnitude, r will be at π/4 angle from either p and q So r will be at 180 deg from

If P Vector Dot Q Vector Is Equal To Pq Then Angle Between P And Q Is Brainly In

Copy Of Chapter 01

Mathematics, a variety of terminology is used to express p !(435) so the new momentum E P= (436) 2 is just proportional to the energy, while Qis a cyclic variable Is this transformation canonical?If q is the mean proportional between p and r prove that p2 – q2 r2 = q41/p2 – 1/q2 1/r2 0 votes 45k views

What Is The Angle Between P Q And P Q Youtube

If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora

We can nd a generating function F = F 1 (q;Q) by dividing the old variables p = m!cot(Q) (437) q This gives us @F 1 p= 1 F @qHave you registered for the PREJEE MAIN PREAIPMT 16?P and q are true separately;

The Angles Between P Q And P Q Will Be Youtube

Semantic Segmentation Of Surface From Lidar Point Cloud Springerlink

P → q (p implies q) (if p then q) is the proposition that is false when p is true and q is false and true otherwise Equivalent to finot p or qfl Ex If I am elected then I will lower the taxes If you get 100% on the final then you will get an A p I am elected q I will lower the taxes Think of it as a contract, obligation or pledgeP then q" or "p implies q", represented "p → q" is called a conditional proposition For instance "if John is from Chicago then John is from Illinois" The proposition p is called hypothesis or antecedent, and the proposition q is the conclusion or consequent Note that p → q is true always except when p is true and q is false 90^@ Given, vec P vec Q=vec R So, we can write, vec R = sqrt(P^2Q^2 2PQ cos theta),where theta is the angle between the two vectors Or, R^2 =P^2 Q^2 2PQ cos theta Given, P^2 Q^2 = R^2 So, R^2 = R^2 2PQ cos theta Or, 2PQ cos theta =0

Find Angle Between P Vector And Q Vector If Resultant Is Given By R 2 P 2 Q 2 Physics Topperlearning Com 40y2cnxx

Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube

If vec P vec Q = PQ , then angle between vec P and vec Q isExplanation The form of a modus tollens argument resembles a syllogism, with two premises and a conclusion If P, then Q Not Q Therefore, not P The first premise is a conditional ("ifthen") claim, such as P implies QThe second premise is an assertion that Q, the consequent of the conditional claim, is not the case From these two premises it can be logically concluded that P,Solution 2 Examine every possible case in which the statement (p!q) ^(q!p) may not have the same truth value as p$q Case 1 Suppose (p!q)^(q!p) is false and p$qis true There are two possible cases where (p!q) ^(q!p) is false Namely, p!qis false or q!p is false (note that this covers the possibility both are false since we use the

Cs Umd Edu

What Is The Angle Between P Q And P Q Vectors Quora

Paper by Super 30 kash Institute, powered by embibe analysisImprove your score by 22% minimum while there is still timeThe conditional of q by p is "If p then q " or " p implies q " and is denoted by p q It is false when p is true and q is false; In classical propositional logic, "if P then Q" is equivalent to "not P or Q" and to "not (P and not Q) and to "P only if Q" 'Unless' is taken to be equivalent to the inclusive 'or' So in your two examples, "if P then Q" is not equivalent to "P unless Q" nor is it equivalent to "P or not Q"

In Pqr If Pq Qr And L M And N Are The Mid Points Of The Sides Pq Qr And Rp Respectively Prove That Ln Mn Mathematics Topperlearning Com 2liv2euss

If P Q P Q Then

R = 2 2 P Q tan P Q M Result 2 If the forces are equal (ie) Q = P, then R P 2P cosD P 2 2P 2 1 cosD = 2 2 22cos 2 D P = 2P 2 cos D D tanM = sin 2 2 cos 2 cos 2 2 sin 1cos sin 2D D D D P P = 2 tan D ie) 2 DP→Q means If P then Q ~R means NotR P ∧ Q means P and Q P ∨ Q means P or Q An argument is valid if the following conditional holds If all the premises are true, the conclusion must be true Some valid argument forms (1) 1 P 2 P→Q C Therefore, QP Q Q AE CE Result 1 If the forces P and Q are at right angles to each other, then D = 90o;

Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com

Quaternion Wikipedia

 Given that p vectorq vector=rvector and pq=rthen angle between p vector & q vector 5902 Views if p tends(~p^~q) is false,then the truth value of p and q are respectivelyOtherwise it is true Contrapositive The contrapositive of a conditional statement of the form "If p then q " is "If ~ q then ~ p " Symbolically, the contrapositive of p1) Zero 2) tan1 (P/Q) 3) tan1 (Q/P) 4) tan1 (P/Q)(P

Ketteringschools Org

If Vec P Vec Q Pq Then Angle Between Vec P And Vec Q Is Youtube

"if p, then q" The truth value of p q is false if p is true and q is false Else, it is true 15 More on Conditional Statement •In the proposition p q, –p is called the hypothesis, or the premise –q is called the conclusion •Many arguments in mathematical reasoningTherefore if p is true then q and r are true ∴ (¬p∨¬q) e negation of(p q) dot (p q) = p^2 q^2 = 0, because p and q have equal lengths Since the dot product between two vectors is the product of their lengths times the cosine of the angle between them, this means that the cosine is 0, so the angle is 90 degrees

Clark Shawnee K12 Oh Us

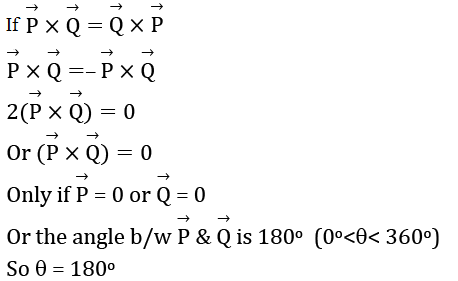
If P X Q Q X P The Angle Between P And Q Is Theta 0o Theta 360o The Value Of Theta Will Be

Now, if p and q are atomic statements, then we do not have p ⇒ q p does not logically imply q, because we can set p to true and q to false However, when describing a world, we can still use p → q For example, we can say that 'If there is smoke, then there is fire' Using p for 'there is smoke', and q for 'there is fire', we can write Resultant of two vectors P & Q is inclined at 45° to either of them What is the magnitude of the resultant asked in Physics by KumariMuskan ( 339k points)

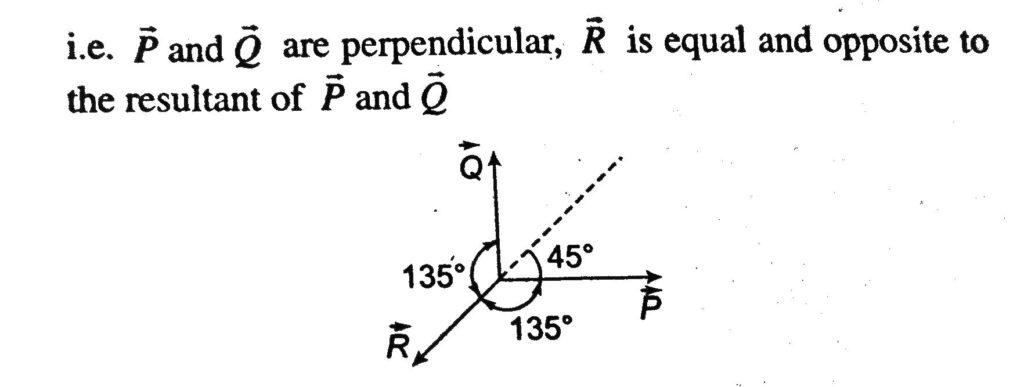
Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And

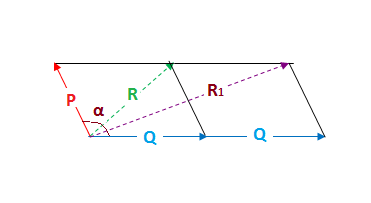
The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Perpendicular To P Then R Is Equal To Socratic

Triangle Congruence Postulates Mathematics For General Education Studocu

Two Vectors P And Q Have Equal Magnitudes If The Magnitude Of Vector P Q Is N Times The Magnitude Of Vector P Q Sarthaks Econnect Largest Online Education Community

Classroomweb Pusd11 Net

Ncert Exemplar Solutions For Class 7 Maths Chapter 5 Lines And Angles Available In Free Pdf

9 At What Angle Do The Two Forces P Q And P Q Act So That The Resultant Is 3p Q Ans 60

What Is The Angle Between P And The Cross Product Of P Q And P Q

Mrl Ucsb Edu

Citeseerx Ist Psu Edu

Of 45 With A If H1 2 Units Then Ais A 13 B Physics

Niagara K12 Wi Us

Given That P Q R If Pvector Qvector Rvector Then The Angle Between Pvector And Rvector Is 81 If Pvector Qvector Rvector 0 The The Angle Between Pvector And Rvector Is What Is The Relation Between 81

Murrieta K12 Ca Us

If Vecp Vecq Pq Then Angle Between Vecp And Vecq Is

If P Q R And P Q R The Ratio Of Angles Between P Amp R To P Amp Q Is Brainly In

Washoeschools Net

Quadrilateral Wikipedia

If Vectors P Q And R Have Magnitude 5 12 And 13 Units And Overrightarrow P Overrightarrow Q Overrightarrow R Then Angle Between Q And R Is Snapsolve

Arxiv Org

Cbse Online

What Is The Angle Between P And Q If Vector P Vector Q Vector P Vector Q Quora

If Vector P Vector Q P Q Then The Angle Between P And Q Is Maths Vector Algebra Meritnation Com

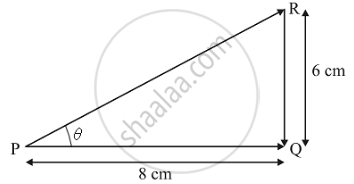
An Ant Travels A Distance Of 8 Cm From P To Q And Then Moves A Distance Of 6 Cm At Right Angles To Pq Find Its Resultant Displacement Science Shaalaa Com

15 If Vectors P Q And R Have Magnitudes 5 12 And 13 Unit Scholr

Benson K12 Mn Us

If P Q P Q What Is The Angle Between P And Q Quora

C 45 Q 25 If P Q Pq Then Angle Between Phu Q 15 B 30 A 0 D 60 Q 26 Two Constant Forces F 22 3j 3k N And F I

Find The Unit Vector In The Direction Of Vector Pq Where P And Q Are

Arxiv Org

Www2 Fairmontstate Edu

Why Trisecting The Angle Is Impossible By Panda The Red Cantor S Paradise

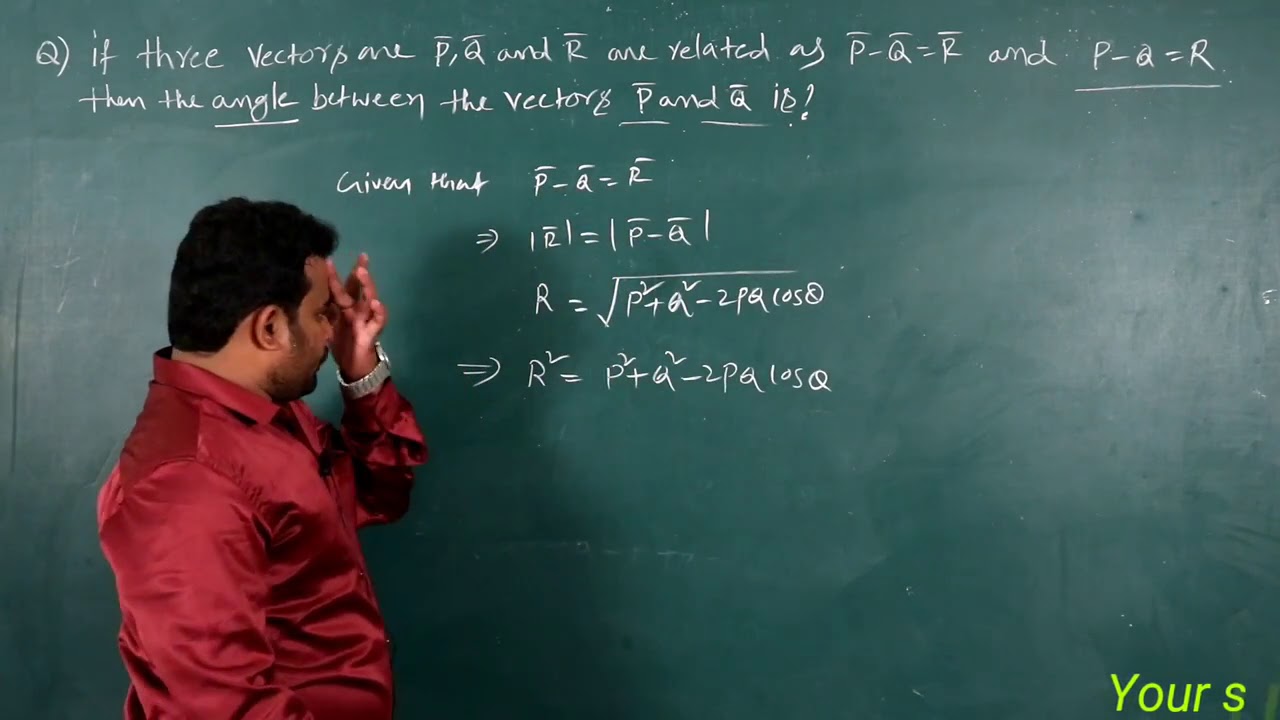
If P Q R Then Angle Between P Q Is Youtube

Shakopee K12 Mn Us

If In Two D Pqr Ab Qr Pr Ca Pq Then Studyrankersonline

A Discrete Dendrite Dynamics Model For Epitaxial Columnar Grain Growth In Metal Additive Manufacturing With Application To Inconel Sciencedirect

In Dpqr Pd Qr Such That D Lies On Qr If Pq A Pr B Qd C And Dr D Then Prove That A B A B

When The Angle Between Forces P And Q Is Alpha Magnitude Of T

1

The Angles Between P Q And P Q Will Be Youtube

5 Inner Product Spaces

Smacmathgeometry Weebly Com

Royalsocietypublishing Org

Defining The Angle Between Vectors Video Khan Academy

Osti Gov

Web Stevens Edu

How To Find The Cosine Of The Angle Between The Plane Through 𝑃 3 0 0 𝑄 0 7 0 And 𝑅 0 0 6 And The 𝑦𝑧 Plane Mathematics Stack Exchange

Find The Angle Between Two Vectors P Vector And Q Vector If Resultant Of The Vector Is Given By R 2 Brainly In

Entropy Free Full Text An Elementary Introduction To Information Geometry Html

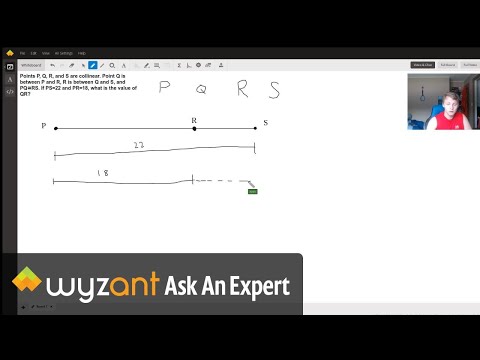
Points P Q R And S Are Collinear Point Q Is Between P And R R Is Between Q And S And Pq Rs If Ps 22 And Pr 18 What Is The Value Of

Ualberta Ca

Solved 162 9 Given That P 0 R And P2 Q2 R2 The Angle Between P And Q Is Donu 1 O 4 Tt

If P Q R And P Q Sqrt 3 And R 3 Then The Angle Between P And Q Is

Cohengroup Ccmr Cornell Edu

Web Auburn Edu

Maa Ac In

Sensors Free Full Text An Energy Scaled And Expanded Vector Based Forwarding Scheme For Industrial Underwater Acoustic Sensor Networks With Sink Mobility Html

Louisianabelieves Com

The Resultant Of A

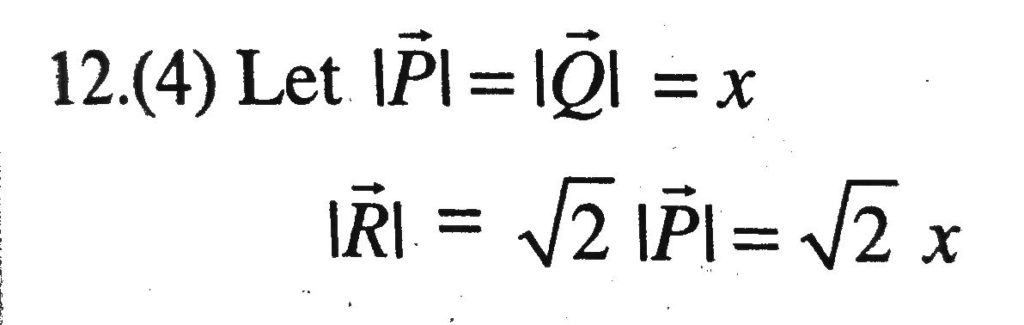
Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And

If P Q R And P Q R The Ratio Of Angles Between P And R And P And Q Physics Motion In A Plane Meritnation Com

Parts Of A Circle

Math Kit Edu

What Is Angle Between P Q And P Cross Q Brainly In

If P Q Pq Then Angle Between P And Q Is Allen Module Exercise Solutions Question 58 Youtube

If P Q P Q And O Is The Angle Between P And Q Then A 0 00 B 0 900 C P 0

Projecteuclid Org

Ucd Ie

Whsd K12 Pa Us

Optics History Applications Facts Britannica

If Vec P Xx Vec Q Pq Then The Angle Between Vec P And Vec

Pearson Com

Points P Q R And S Are Collinear Point Q Is Between P And R R Is Between Q And S And Pq Rs If Ps 22 And Pr 18 What Is The Value Of